02-04 The Larmor Equation

A mechanical analog to the magnetic nature of the nucleus is that it is a spinning mass with a small net positive charge. Because of the motion of the electric char­ge, a small magnetic field is created.

In the presence of an external magnetic field, the behavior can be compared with that of a spinning top (Figure 02-07).

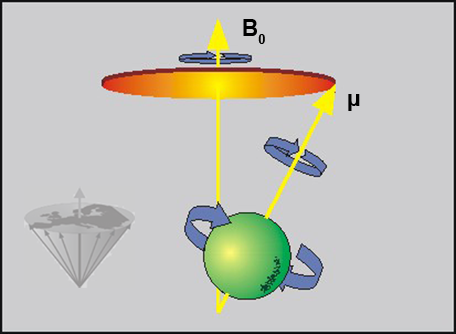
Figure 02-07: A spinning mass with a net positive charge will create a small magnetic moment μ (or "spin"). In the presence of an external field, B0, the moment will precess around the di­rec­tion of the external field.

When the spinning top is submitted to the gravitation of the earth, its motion is com­plex: it rotates around its own axis and precesses around the direction of the earth. In this later motion, the axis of the spinning top is tilted with respect to the direction of the gravitation.

If gravitation were absent, precession would not happen. The magnetic pro­per­ties of the atomic nuclei make them precess around the external field.

Actually, for protons, two cones of precession exist: one for the nuclei in the state of low energy (represented in Figure 02-07) and another one in the op­po­site direction for the nuclei in the high energy state.

The frequency ω of this precessing motion is given by the following equation, called the Larmor equation:

ω = γ × B₀

ω is the angular Larmor frequency (unit: MHz), γ is the gyromagnetic ratio (unit: MHz/T), which describes the ratio of mechanic and magnetic properties of the nucleus and depends on the type of nucleus.

B0 is the strength of the magnetic field in Tesla (T).

This is one of the few fundamental equations to understand NMR and MR ima­ging, its technology and its applications.

In Table 02-02, the values for some nuclei commonly used in MR imaging and MR spectroscopy are given. Note that two nuclei with different gyromagnetic ra­tios will precess with different Larmor frequencies if placed in the same mag­ne­tic field. Con­se­quent­ly, their resonance frequencies will be different.

Table 02-03 shows an overview of typical excitation frequencies in MR ima­ging and magnetic field strengths for hydrogen, fluorine, phosphorus, and so­di­um nuclei.

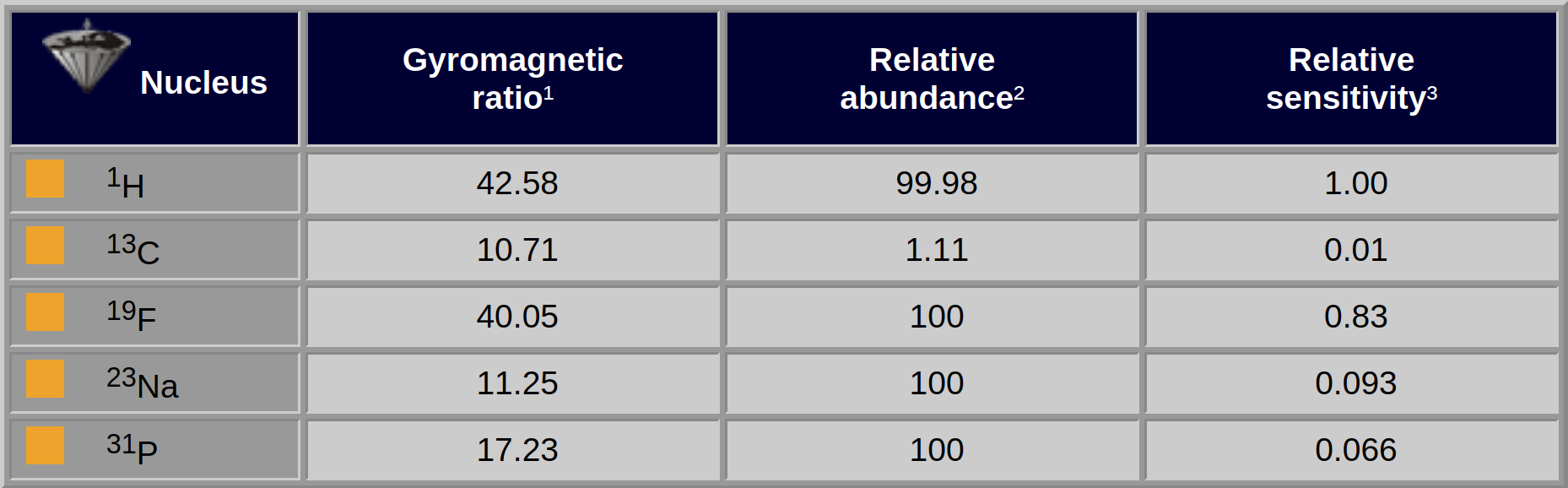
Table 02-02:
Magnetic values for some common elements.
¹Gyromagnetic ratio: MHz/T; to obtain the resonance frequency, one multiplies the cited number with the field strength. ²Relative abundance: per­cen­ta­ge. ³Sensitivity: at constant field, taking into account their relative abundance.

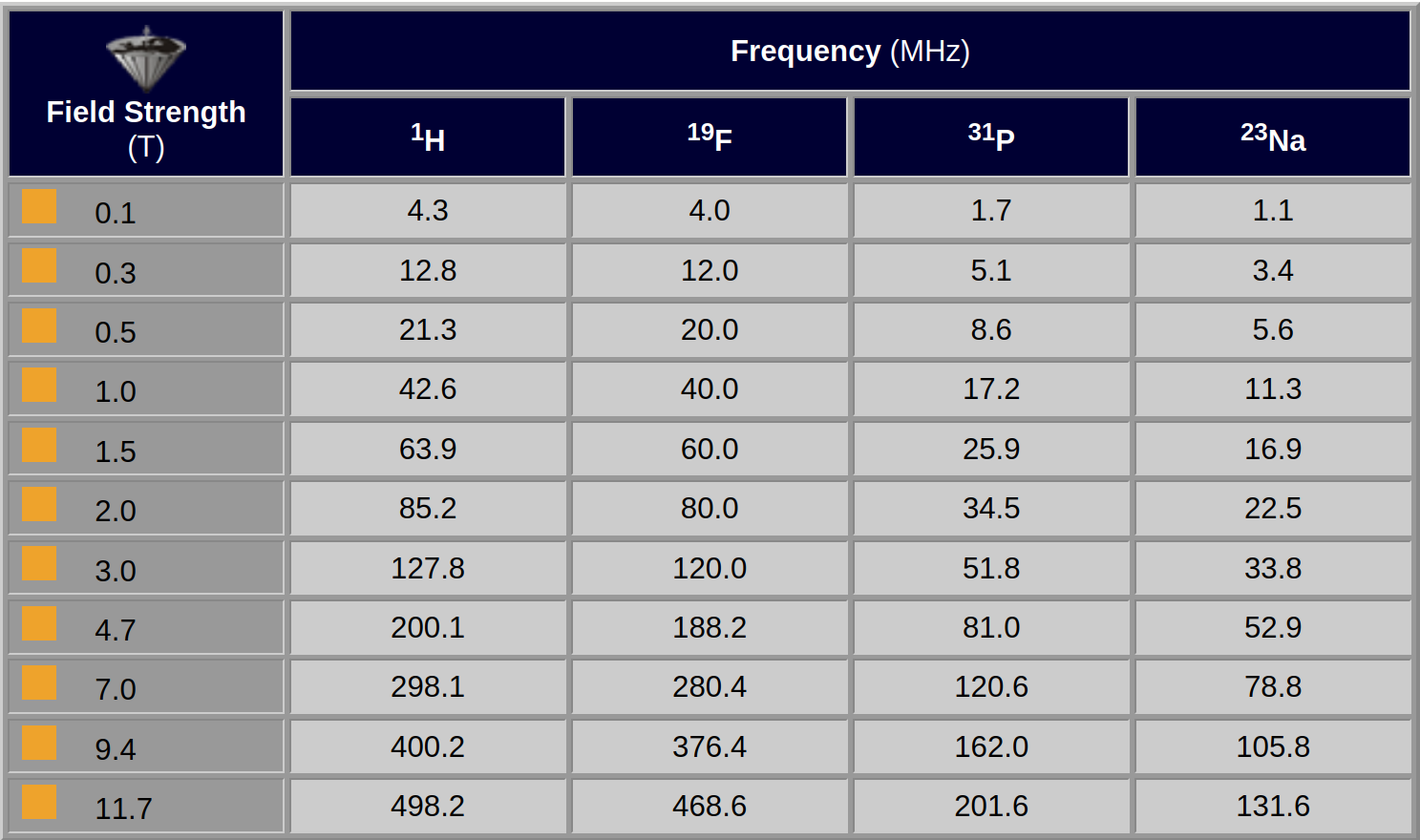
Table 02-03:
Dependence of field strength and frequency for some commonly used nuclei (rounded values).